基础课目 >>> 数学 >>> 课程介绍 >>>

美国中小学数学课程介绍

A + LS数学课程是根据全国数学教师协会（NCTM）设定的一系列标准而开发的一套综合性的，系统性的数学教材，包括了一年级到十二年级的全部课程。它对每个数学的教学主题都提供了丰富的图文并茂的内容。直接在计算机屏幕显示科学，规范的计算方法，以协助学生完成作业。所有学习主题都提供丰富的教程支持，和相关的必须掌握的教学标准紧密相连。 使用A + LS提供的学习指南，练习测试，精通测试及作文四步操练方法，成功地帮助学生引入一个概念，完整地解释它，并反复使用例子来加强对概念的理解。

高年级的数学主题让学生更有机会回答问题，并通过互动反馈，以提高他们对概念的理解。学生充分发展他们的常用技能，心算，估算，以及使用不同方法来解决问题的能力，学习检查答案是否合理的判断能力。很多课程还要求学生通过写短文让学生展示自己解决问题的思考过程和结果。

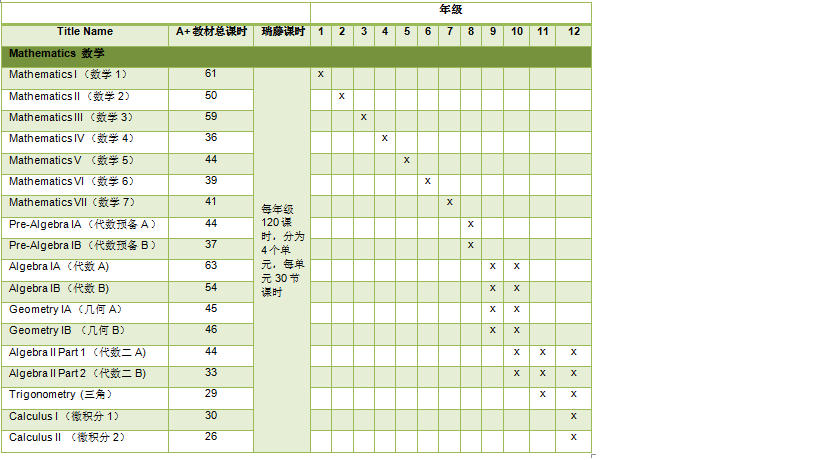
瑞藤教育根据A+教材制定了各年级数学课程，由于课时限制，每个年级共设置120课时，分为四个单元，每单元30课时。根据学生的英语水平，实际授课进度会因人而异有快有慢。如果学生进度较快，则可提前进入下个单元，进度较慢的学生可以通过重新选定该单元已完成剩下内容。

1.  数学I

数学I主要注重数学概念的介绍。课程涵盖数字​​和计数，数字排序，垂直加减法，序号，数量的估计，数字的组合，应用题。此外，用句子表达加减的概念，确定解决问题所需要的加减符号，能阅读和创建图表，识别硬币和数硬币，测量长度，重量，温度，识别时间，识别三维图像，对称性，以及分数。

数学I还包括其他主题，如：

用横坐标做加法
数字模式
以十为单位计数
成比例的数字组合

2.  数学II

数学II主要在以下几个方面加强数学技能：数字和计数，奇数和偶数，钱和钱的使用战略，图形，加法和减法，使用计算器，测量，识别时间，解决应用题，分数，和估算。还向学生介绍测量周长，对称的物体，概率，解决问题的策略，逻辑，有序对, 乘法和除法。课程还教授从数字时钟或模拟时钟里读取时间。

数学II还包括其他的主题，如：

复杂的图表
序号
使用计算器
测量重量
测量温度
介绍乘法
介绍除法
识别硬币值

3.  数学III

数学三主要涵盖以下主题：重组数字的加法和减法，纸币和硬币计数，使用数线，心算，用标准和非标准单位测量长度，使用条形图，使用计算器，找平均数，中位数，众和范围，估算和测量容量，时间和重量，阅读摄氏和华氏温度，三个数乘法，测量面积，被十和百整除，加减分数，使用象形文字解决问题，小数，概率，平面图形，坐标，识别面，边和角，学习运用逻辑推理。

数学三还包括其他的主题，如：

非标准测量
模式和计算
结论和预测
多步骤的应用题
线，射线，和段


4.  数学IV

数学四涵盖的内容包括分组的加法和减法，奇数和偶数，乘法和除法问题，用钱，五个步骤解决问题的方法，使用日历，温度，小数写入到十和百分之位置，线段和角度，地图和坐标比较，图表类型的比较，根据所有信息制订应用题。

5.  数学V

数学五涵盖指数，标准，扩大，数字和用文字形式写数字，写小数，小数加减，属性加成，五步思维计划，两三位数乘法，调查，使用线和圆圈的图表，维恩图，最小公倍数，单位长度，经过的时间，线和角度，圆，周长，圆周，尖塔，和概率。

6.  数学 VI

数学六在下列方面加强数学知识和能力：四舍五入，估计，位值，数字的属性，小数乘法，两位数字除法，素数，等值分数，相吻合，确定变量，解方程，长度，容量和重量单位，温度，线和射线，圆的一部分，周长，正和负的整数，和有序对。

7.  数学VII

数学七涵盖价值，交换，联想，零，一，分配属性，逆运算的因素，数论，混合数字，比例，百分比概念，标记，佣金，解方程步骤，测量长度，质量/重量公制单位，点，角度，计算周长，面积，体积，使用了一些行和图形下令对坐标轴。

8.  代数预备IA  

代数预备IA  是一个完整学期的课程，旨在帮助学生缩小从初中小学基础学习到进入更先进严谨的高中数学课程的差距。代数预备IA 主要内容 都超过标准8年级国家通用数学核心标准。本课程为学生提供一个易于使用的互动学习的网上工具，以鼓励他们完整彻底地解答问题， 并学会检查自己的结果。

9.  代数预备IB

代数预备IB 是一个完整学期继代数预备IA  后的课程。学生进步通过反复教训，为代数和几何的概念奠定了坚实的基础。代数预备IB主要内容 都超过标准8年级国家通用数学核心标准。本课程为学生提供一个易于使用的互动学习的网上工具，以鼓励他们完整彻底地解答问题， 并学会检查自己的结果。

10.  代数IA

 

代数IA是一个完整学期的课程旨在教导学生学习基本的代数概念。课程内容的设计，都超过国家通用数学核心标准：高中代数。代数IA使用的互动学习和现实世界的应用来引导学生，从基本数学概念的理解过渡到对更高深的数学概念的理解，能够分析和解释求解方程和不等式的过程，开发函数，线性方程组的概念。

11.  代数IB

代数IB是一个完整学期的课程旨在教导学生进一步的学习代数概念。课程内容的设计，都超过国家通用数学核心标准：高中代数。本课程使用的交互性和现实世界的应用来吸引学生，从基本数学概念的理解过渡到对更高深的数学概念的理解，如转化指数函数，因式分解，求取平方和平方根，根据图表和收集的数据集进行推算。

12.  几何IA

几何IA是一个完整学期的课程，旨在向学生传授几何的基本概念。本课程是基于国家通用数学核心标准数学几何的第一级。所有课程都运用真实世界的实例，帮助学生理解几何的关键概念。几何IA主题覆盖基本的点，线，面，段和角度的几何概念，然后进步到更加复杂的部分，包括公式，证明，定理，同余定理，比和比例，以及多边形。

13.  几何IB

几何IB是一个完整学期的课程，旨在为后续课程A + LS™几何IA，这是基于国家通用数学核心标准。所有课程都设计运用真实世界的实例，帮助学生理解几何的关键概念。几何IB继续扩大学生的知识，定理，公式，证明。然后课程扩展到包括更复杂的主题，如正弦和余弦，特殊几何形状，几何测量，多维物体和测量。

14.  代数II，第1部分

代数II：第1部分的主题领域包括审查包括实数系的有理数，规则结合和实数相乘，操作顺序，文字和数字连接，通过表情，制定一项计划来解决一个问题，合并同类项，定义和下令对电网的例子，象限，横坐标，定义线性方程组，方程组的图形，三个变量的方程，矩阵乘法，转换点和矩阵变换，多项式的类型，作为指数为零，寻找更高的变数，保分子和解决复杂的有理数。

15.  代数II，第2部分

代数II：第1部分的延续，这个课程包括平方根，自由基，复杂的纯数和虚数，解决和保，识别和求解一元二次方程，改写方程式，求解图形抛物线，环形部件和公式，双曲线，图形二次关系和不平等，反函数，复利问题，数字序列，识别σ，公比，有限系列，以及解决阶乘问题。

16.  三角函数

三角函数覆盖角度，角度术语，参考角度，定义正弦，余弦，正切和正割的定义，余割，余切，计算直角三角形边，用三角来解决现实世界的问题，正弦和余弦法，对称的定义，证明三角恒等式，求解正弦，余弦，正切的总结和差异，使用共同的功能标识，能画三角函数的图形，主值，弧长，扇形面积，简谐运动和频率。

17.  微积分I

微积分涵盖计算x值和其相应的值，限制，符号，连续函数，渐近线，消极和积极的无穷大，图形切线，割线，割线合作，衍生工具，莱布尼茨符号，常数函数及衍生工具，产品，衍生工具的功能，为正弦波，加速度作为衍生工具的速度，函数在闭区间的最高和最低值，使用相关的比利来确定圆锥体的体积，确定图形数据，不定积分负指数的倒数。

18.  微积分II

微积分的I课程的持续，微积分II主要涵盖积分符号，微积分，不定积分和不定积分基本定理，代换积分法，自然对数，交点图表区域，应用程序的积分包括卷旋转轴，电弧长度，表面积和工作，静力，逆功能，包括自然指数函数，指数函数和对数函数的其他基地，指数增长和衰减，和反三角函数。